
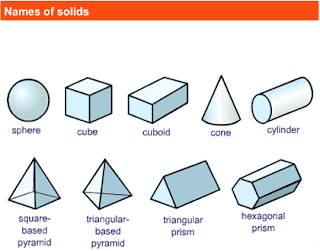
There are 12 edges on a cube, which are all the same length. All of its edges are the same length.Įach of the 6 faces of a cube is square-shaped because all of its edges are the same size. Marking the faces, edges and vertices as you count them is important as it can be easy to count them twice or miss one out.Ī cube has 6 faces, 12 edges and 8 vertices. You could put a sticker or piece of plasticine on each vertex as you count it. You can mark each edge as you count it by drawing a line on each one. You can colour in each face a different colour, or write a number from 1 – 6 on each square face. When teaching this topic, it can be helpful to count the number of each property on the net before assembling it. Alternatively, there are some online interactive 3D shapes in the practice section above that you can use to count the faces, edges and vertices. There are also printable nets for each 3D shape above that can be downloaded and assembled to accompany this lesson. When teaching the properties of 3D shapes, it is worth having a physical item to look at as you identify and count each property. All three dimensional shapes have the the three dimensions of length, width and depth.Ī shape is 3D if it can be picked up and held in real-life. The following table lists the number of faces, edges and vertices for some common 3D shapes:ģD is short for three-dimensional. The poster below shows the faces, edges and vertices of 3D shapes labelled on a cube. Vertices are the corners of a 3D shape formed where two or more edges meet.įor example, a cube has 6 faces, 12 edges and 8 vertices.Edges are the lines where two faces on a 3D shape meet.Faces are the flat or curved surfaces that make up the outside of a 3D shape.The properties of 3D shapes are faces, edges and vertices.


 0 kommentar(er)
0 kommentar(er)
